Diferencia entre revisiones de «Las ciencias formales»
(Página creada con «El origen de las ciencias formales ¿Cuándo comenzó la ciencia? Una de las dificultades para responder a esta pregunta reside en cómo caracterizar esa forma de conocimie...») |
|||
| (No se muestran 14 ediciones intermedias del mismo usuario) | |||
| Línea 1: | Línea 1: | ||
El origen de las ciencias formales | ==El origen de las ciencias formales== | ||
¿Cuándo comenzó la ciencia? Una de las dificultades para responder a esta pregunta reside en cómo caracterizar esa forma de conocimiento que llamamos “ciencia”. Los filósofos de la ciencia han dado concepciones diversas de lo que ésta es. | ¿Cuándo comenzó la ciencia? Una de las dificultades para responder a esta pregunta reside en cómo caracterizar esa forma de conocimiento que llamamos “ciencia”. Los filósofos de la ciencia han dado concepciones diversas de lo que ésta es. | ||
Podríamos reformular la pregunta así: ¿Cuándo y dónde apareció algo suficientemente parecido a lo que hoy llamamos “ciencia”? Los historiadores (al menos los occidentales: la ciencia, como hoy la conocemos, es una creación de Occidente) responderían “La ciencia comenzó en la antigua Grecia”. | Podríamos reformular la pregunta así: ¿Cuándo y dónde apareció algo suficientemente parecido a lo que hoy llamamos “ciencia”? Los historiadores (al menos los occidentales: la ciencia, como hoy la conocemos, es una creación de Occidente) responderían “La ciencia comenzó en la antigua Grecia”. | ||
Aquellos griegos se reconocieron herederos de los conocimientos de las espléndidas civilizaciones de Babilonia y Egipto pero, además de incrementarlo enormemente, introdujeron la necesidad de sistematizarlo y justificarlo explícitamente. Los documentos históricos no dan indicios de que egipcios y babilonios hayan sentido una necesidad similar. | Aquellos griegos se reconocieron herederos de los conocimientos de las espléndidas civilizaciones de Babilonia y Egipto pero, además de incrementarlo enormemente, introdujeron la necesidad de sistematizarlo y justificarlo explícitamente. Los documentos históricos no dan indicios de que egipcios y babilonios hayan sentido una necesidad similar. | ||
La ciencia según Aristóteles | |||
==La ciencia según Aristóteles== | |||
Aristóteles de Estagira (Aristóteles) (siglo IV a. C.) fue un filósofo importante en su tiempo, pero es especialmente importante cuando consideramos la influencia que llegaría a tener más adelante. | Aristóteles de Estagira (Aristóteles) (siglo IV a. C.) fue un filósofo importante en su tiempo, pero es especialmente importante cuando consideramos la influencia que llegaría a tener más adelante. | ||
En la Baja Edad Media se impone la filosofía escolástica que integra en un mismo sistema las ideas de Aristóteles con las enseñanzas de la Biblia y la doctrina católica. Y se suponía que Aristóteles –“El Maestro”, como solía llamárselo– era casi tan infalible como la Biblia. | En la Baja Edad Media se impone la filosofía escolástica que integra en un mismo sistema las ideas de Aristóteles con las enseñanzas de la Biblia y la doctrina católica. Y se suponía que Aristóteles –“El Maestro”, como solía llamárselo– era casi tan infalible como la Biblia. | ||
| Línea 20: | Línea 21: | ||
El primer ejemplo de aplicación de estas ideas lo encontramos en la geometría que construyó Euclides, que vivió en Alejandría hacia el año 300 a. C. | El primer ejemplo de aplicación de estas ideas lo encontramos en la geometría que construyó Euclides, que vivió en Alejandría hacia el año 300 a. C. | ||
La geometría euclidiana | ==La geometría euclidiana== | ||
El tratado de Euclides conocido como los Elementos es uno de las obras más exitosas de la historia; hasta el siglo XIX fue usado como libro de texto y su modo de exponer la ciencia, lo que hoy llamamos “sistema axiomático”, fue imitado en las disciplinas más diversas (con mayor o menor éxito). | El tratado de Euclides conocido como los Elementos es uno de las obras más exitosas de la historia; hasta el siglo XIX fue usado como libro de texto y su modo de exponer la ciencia, lo que hoy llamamos “sistema axiomático”, fue imitado en las disciplinas más diversas (con mayor o menor éxito). | ||
Los primeros seis de sus trece libros tratan sobre geometría plana y comienzan con 23 definiciones de los términos que emplea, cinco postulados y los axiomas (entre cinco y once, según los distintos comentaristas). Luego da las demostraciones de 465 teoremas. Algunos de esos teoremas nos resultan tan obvios que no parece que fuera necesario demostrarlos, por ejemplo, | Los primeros seis de sus trece libros tratan sobre geometría plana y comienzan con 23 definiciones de los términos que emplea, cinco postulados y los axiomas (entre cinco y once, según los distintos comentaristas). Luego da las demostraciones de 465 teoremas. Algunos de esos teoremas nos resultan tan obvios que no parece que fuera necesario demostrarlos, por ejemplo, | ||
| Línea 28: | Línea 29: | ||
Esta geometría fue considerada como, simplemente, la geometría que describe el espacio en el que vivimos. Los filósofos racionalistas la consideraron el ejemplo más claro de que podemos adquirir conocimiento del mundo empleando solamente nuestra razón: no hace falta hacer experimentos para demostrar las afirmaciones de la geometría. | Esta geometría fue considerada como, simplemente, la geometría que describe el espacio en el que vivimos. Los filósofos racionalistas la consideraron el ejemplo más claro de que podemos adquirir conocimiento del mundo empleando solamente nuestra razón: no hace falta hacer experimentos para demostrar las afirmaciones de la geometría. | ||
El quinto postulado | ==El quinto postulado== | ||
Se esperaba que los postulados | Se esperaba que los postulados expresaran verdades tan evidentes que estuviera claro que no es necesario demostrarlos; por ejemplo, el primer postulado dice: | ||
Desde un punto a otro se puede trazar una línea recta | Desde un punto a otro se puede trazar una línea recta | ||
Pero ese no parece ser el caso del quinto postulado: | Pero ese no parece ser el caso del quinto postulado: | ||
Si una línea recta al caer sobre otras dos forma ángulos en el interior y del mismo lado de la secante menores [su suma] que dos rectos [180 º], las dos rectas, | Si una línea recta al caer sobre otras dos forma ángulos en el interior y del mismo lado de la secante menores [su suma] que dos rectos [180 º], las dos rectas, indefinidamente, se encuentran en aquella parte en la cual los ángulos son menores que dos rectos. | ||
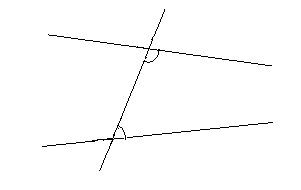
[[Archivo:Euclides-1.jpg|right]] | |||
Así lo formuló Euclides. No es sólo la dificultad de traducir fielmente algo escrito hace más de dos milenios; simplemente, no tiene la “obviedad” de los otros cuatro postulados; es difícil entenderlo sin la ayuda de un dibujo. | Así lo formuló Euclides. No es sólo la dificultad de traducir fielmente algo escrito hace más de dos milenios; simplemente, no tiene la “obviedad” de los otros cuatro postulados; es difícil entenderlo sin la ayuda de un dibujo. | ||
Muchos matemáticos pensaron, entonces, que no se trataba de un auténtico postulado sino de un teorema que podría ser demostrado a partir de los otros cuatro. A lo largo de los siglos fueron varios los matemáticos que buscaron esa demostración. El primero fue, quizá, Posidonio de Apamea en el siglo I a. C. Y lo consiguió, pero a costa de introducir otro postulado: | Muchos matemáticos pensaron, entonces, que no se trataba de un auténtico postulado sino de un teorema que podría ser demostrado a partir de los otros cuatro. A lo largo de los siglos fueron varios los matemáticos que buscaron esa demostración. El primero fue, quizá, Posidonio de Apamea en el siglo I a. C. Y lo consiguió, pero a costa de introducir otro postulado: | ||
| Línea 41: | Línea 45: | ||
¿Es esta afirmación necesariamente verdadera? | ¿Es esta afirmación necesariamente verdadera? | ||
Las geometrías no euclidianas | ==Las geometrías no euclidianas== | ||
No son infrecuentes en la historia de la ciencia los casos de descubrimientos independientes y casi simultáneos. En el siglo XIX Carl Friedrich Gauss, János Bolyai y Nikolai Lobachevsky también intentaron demostrar el quinto postulado de Euclides empleando la misma estrategia: la demostración por reducción al absurdo. Se trata de tomar como premisas los cuatro primeros postulados y la negación del quinto, que en este caso fue | No son infrecuentes en la historia de la ciencia los casos de descubrimientos independientes y casi simultáneos. En el siglo XIX Carl Friedrich Gauss, János Bolyai y Nikolai Lobachevsky también intentaron demostrar el quinto postulado de Euclides empleando la misma estrategia: la demostración por reducción al absurdo. Se trata de tomar como premisas los cuatro primeros postulados y la negación del quinto, que en este caso fue | ||
Por un punto exterior a una recta pasa más de una paralela a dicha recta | Por un punto exterior a una recta pasa más de una paralela a dicha recta | ||
Luego se intenta deducir de ellos un enunciado de la forma “p y no p” (“p ∧ ~p”, siendo p cualquier enunciado); esta es una contradicción, que es necesariamente falsa; si se logra hacerlo, queda demostrado que el quinto postulado puede deducirse a partir de los otros cuatro. | Luego se intenta deducir de ellos un enunciado de la forma “p y no p” (“p ∧ ~p”, siendo p cualquier enunciado); esta es una contradicción, que es necesariamente falsa; si se logra hacerlo, queda demostrado que el quinto postulado puede deducirse a partir de los otros cuatro. | ||
Consiguieron demostrar teoremas muy extraños pero no encontraron ninguna contradicción. Sin embargo no creyeron haber fracasado sino todo lo contrario: creyeron que los primeros cuatro postulados de Euclides y la negación del quinto constituyen una geometría distinta, una geometría que describe un mundo en el cuál, a diferencia de la geometría euclidiana, por un punto exterior a una recta pasan infinitas paralelas a dicha recta, la suma de los ángulos interiores de un triángulo vale menos de 180 º y la relación entre la circunferencia y su diámetro es mayor que π; un mundo que no es éste y que no cabe en nuestra imaginación, pero que no es un mundo lógicamente imposible. Hoy se la conoce como geometría de Lobachevsky (fue el primero en publicarla, en 1829). | Consiguieron demostrar teoremas muy extraños pero no encontraron ninguna contradicción. Sin embargo no creyeron haber fracasado sino todo lo contrario: creyeron que los primeros cuatro postulados de Euclides y la negación del quinto constituyen una geometría distinta, una geometría que describe un mundo en el cuál, a diferencia de la geometría euclidiana, por un punto exterior a una recta pasan infinitas paralelas a dicha recta, la suma de los ángulos interiores de un triángulo vale menos de 180 º y la relación entre la circunferencia y su diámetro es mayor que π; un mundo que no es éste y que no cabe en nuestra imaginación, pero que no es un mundo lógicamente imposible. Hoy se la conoce como geometría de Lobachevsky (fue el primero en publicarla, en 1829). | ||
En 1854 Bernhard Riemann desarrolló otra geometría no euclidiana en la que por un punto exterior a una recta no pasa ninguna paralela a dicha recta, la suma de los ángulos interiores de un triángulo vale más de 180 º y la relación entre la circunferencia y su diámetro es menor que π; en esta geometría el espacio es finito pero sin límites, sin bordes, y también sin centro. No es el espacio finito de la cosmología aristotélico-ptolemaica que sí tiene un límite –la esfera de las estrellas fijas– y un centro –el lugar donde está la Tierra–. | En 1854 Bernhard Riemann desarrolló otra geometría no euclidiana en la que por un punto exterior a una recta no pasa ninguna paralela a dicha recta, la suma de los ángulos interiores de un triángulo vale más de 180 º y la relación entre la circunferencia y su diámetro es menor que π; en esta geometría el espacio es finito pero sin límites, sin bordes, y también sin centro. No es el espacio finito de la cosmología aristotélico-ptolemaica que sí tiene un límite –la esfera de las estrellas fijas– y un centro –el lugar donde está la Tierra–. | ||
Muchos matemáticos de la época consideraron a las geometrías no euclidianas como meros juegos que no eran dignos de aparecer en publicaciones científicas; las tildaron de “caricatura geométrica”, de “manifestación morbosa de la geometría”. Gauss, el primero que tuvo la idea, fue precavido y no publicó nada “por temor al griterío de los beocios [tontos]”. Evidentemente la geometría verdadera tenía que ser la de Euclides; las otras no podían ser más que meros “ejercicios lógicos”. | Muchos matemáticos de la época consideraron a las geometrías no euclidianas como meros juegos que no eran dignos de aparecer en publicaciones científicas; las tildaron de “caricatura geométrica”, de “manifestación morbosa de la geometría”. Gauss, el primero que tuvo la idea, fue precavido y no publicó nada “por temor al griterío de los beocios [tontos]”. Evidentemente la geometría verdadera tenía que ser la de Euclides; las otras no podían ser más que meros “ejercicios lógicos”. | ||
El espacio físico | ==El espacio físico== | ||
En nuestro andar por el mundo consideramos el espacio y el tiempo como algo “dado”, como el marco en el que ocurren los hechos que podemos observar y que nos brindan información acerca de cómo es este mundo. El espacio y el tiempo son como la escenografía de una obra de teatro: el marco en el que se desarrolla la acción, que es lo que nos interesa. | En nuestro andar por el mundo consideramos el espacio y el tiempo como algo “dado”, como el marco en el que ocurren los hechos que podemos observar y que nos brindan información acerca de cómo es este mundo. El espacio y el tiempo son como la escenografía de una obra de teatro: el marco en el que se desarrolla la acción, que es lo que nos interesa. | ||
Hasta el siglo XIX, | Hasta el siglo XIX, ése era también el papel del espacio y el tiempo en la investigación científica; no parecía que pudiera irse más allá de la especulación filosófica en estos temas. | ||
Pero sí era posible: en 1915 Albert Einstein publica su teoría general de la relatividad. | |||
Según esta teoría, espacio, tiempo y materia son interdependientes, no existe uno sin los otros. Si es correcta [[teoría del "big bang"]] (que presupone la relatividad einsteiniana) el espacio real, el espacio físico en el cual existimos, es finito pero sin centro ni límites. La mejor aproximación a la geometría del universo considerado como un todo es la geometría de Riemann, no la de Euclides. | |||
¿Cómo puede algo ser finito pero no tener algo en el medio ni terminar en algún lugar? Nuestra intuición nos dice que eso no puede ser, pero, ¿es infalible nuestra intuición?, ¿no nos dice nuestro sentido común que la Tierra es plana y que no se mueve? | ¿Cómo puede algo ser finito pero no tener algo en el medio ni terminar en algún lugar? Nuestra intuición nos dice que eso no puede ser, pero, ¿es infalible nuestra intuición?, ¿no nos dice nuestro sentido común que la Tierra es plana y que no se mueve? | ||
Aceptamos sin protestar que la Tierra es redonda y se mueve alrededor del Sol porque nos lo repitieron varias veces en la época de nuestra vida en la que no se nos ocurriría dudar de lo que nos decía nuestra maestra de la escuela primaria. Los filósofos y los científicos no pueden permitirse esa actitud acrítica; pueden, en cambio, hacer el esfuerzo de reeducar sus intuiciones de sentido común. | Aceptamos sin protestar que la Tierra es redonda y se mueve alrededor del Sol porque nos lo repitieron varias veces en la época de nuestra vida en la que no se nos ocurriría dudar de lo que nos decía nuestra maestra de la escuela primaria. Los filósofos y los científicos no pueden permitirse esa actitud acrítica; pueden, en cambio, hacer el esfuerzo de reeducar sus intuiciones de sentido común. | ||
Pero nuestra intuición tiene un límite. Las teorías de la física moderna, las que aparecieron a principios del siglo XX, la relatividad y la cuántica, nos dicen que la realidad supera las posibilidades de nuestra imaginación. Éste fue uno de los motivos por el que fueron muy resistidas en su momento. Ahora, los científicos aceptan que las teorías científicas que se refieren al mundo pueden ir más allá de nuestra intuición. Es necesario, por supuesto, que sea posible inferir de ellas consecuencias observacionales ( | Pero nuestra intuición tiene un límite. Las teorías de la física moderna, las que aparecieron a principios del siglo XX, la relatividad y la cuántica, nos dicen que la realidad supera las posibilidades de nuestra imaginación. Éste fue uno de los motivos por el que fueron muy resistidas en su momento. Ahora, los científicos aceptan que las teorías científicas que se refieren al mundo pueden ir más allá de nuestra intuición. Es necesario, por supuesto, que sea posible inferir de ellas consecuencias observacionales ([[El método hipotético- deductivo]]) que permitan someterlas a [[contrastación]]; eso es lo que las permite calificarlas como ciencias fácticas. | ||
Es interesante el caso del “evidente” axioma 5 de Euclides: “El todo es mayor que la parte”. En 1874, Georg Cantor mostró que esa afirmación no puede justificarse cuando se trata de conjuntos infinitos, tema de casi toda la matemática. Por chocante que suene, debe admitirse que hay tantos números naturales (el todo) como números naturales pares (la parte). ¿Por qué habría de extrañarnos que nuestra intuición falle cuando nos las vemos con lo infinito? (También Cantor fue incomprendido por sus contemporáneos; algunos lo trataron de loco, y hasta de blasfemo por intentar introducir en la ciencia el infinito, uno de los misterios de Dios). | Es interesante el caso del “evidente” axioma 5 de Euclides: “El todo es mayor que la parte”. En 1874, Georg Cantor mostró que esa afirmación no puede justificarse cuando se trata de conjuntos infinitos, tema de casi toda la matemática. Por chocante que suene, debe admitirse que hay tantos números naturales (el todo) como números naturales pares (la parte). ¿Por qué habría de extrañarnos que nuestra intuición falle cuando nos las vemos con lo infinito? (También Cantor fue incomprendido por sus contemporáneos; algunos lo trataron de loco, y hasta de blasfemo por intentar introducir en la ciencia el infinito, uno de los misterios de Dios). | ||
Pero, entonces, ¿la geometría de Euclides es falsa? | Pero, entonces, ¿la geometría de Euclides es falsa? | ||
---- | |||
Ciencias formales y ciencias fácticas | Ciencias formales y ciencias fácticas | ||
Si decimos que esto | Si decimos que esto | ||
5 | 5 | ||
es un cinco, deberíamos decir que esto | es un cinco, deberíamos decir que esto | ||
hipopótamo | hipopótamo | ||
es un hipopótamo. Pero no, no decimos que es un hipopótamo, decimos que es un signo que usamos para hablar de los hipopótamos, unos animales grandotes que se bañan en los ríos de África y llegan a vivir hasta 30 años. Con el mismo criterio, entonces, deberíamos decir que “5” es un signo que usamos para referirnos... ¿a los cincos? ¿Y cómo son los cincos? ¿Son grandes o pequeños?, ¿dónde se bañan los cincos?, ¿cuánto tiempo vive un cinco? | es un hipopótamo. Pero no, no decimos que es un hipopótamo, decimos que es un signo que usamos para hablar de los hipopótamos, unos animales grandotes que se bañan en los ríos de África y llegan a vivir hasta 30 años. Con el mismo criterio, entonces, deberíamos decir que “5” es un signo que usamos para referirnos... ¿a los cincos? ¿Y cómo son los cincos? ¿Son grandes o pequeños?, ¿dónde se bañan los cincos?, ¿cuánto tiempo vive un cinco? | ||
El desarrollo de la lógica y la matemática en la segunda mitad del siglo XIX y principios del XX ha conducido a una distinción tajante entre ciencias formales y ciencias fácticas. Las ciencias formales –la lógica y la matemática– no tienen contenido fáctico, no se refieren a hechos que podamos observar, no dicen nada acerca de la realidad, acerca del mundo. Los cincos no existen en la realidad, al menos no en la realidad en la que encontramos los objetos que existen en el espacio y en el tiempo, que podemos ver y tocar, como los hipopótamos, los ríos de África y el dedo meñique de nuestra mano izquierda. | El desarrollo de la lógica y la matemática en la segunda mitad del siglo XIX y principios del XX ha conducido a una distinción tajante entre ciencias formales y ciencias fácticas. Las ciencias formales –la lógica y la matemática– no tienen contenido fáctico, no se refieren a hechos que podamos observar, no dicen nada acerca de la realidad, acerca del mundo. Los cincos no existen en la realidad, al menos no en la realidad en la que encontramos los objetos que existen en el espacio y en el tiempo, que podemos ver y tocar, como los hipopótamos, los ríos de África y el dedo meñique de nuestra mano izquierda. | ||
| Línea 81: | Línea 93: | ||
es falsa, si es que tiene algún sentido. | es falsa, si es que tiene algún sentido. | ||
Los axiomas de una ciencia formal son, en su conjunto, definiciones implícitas de los términos que contienen. Implícitas y parciales: se puede enriquecer esos términos con significados de los objetos del mundo y así obtener interpretaciones que se referirán al mundo. Si esas interpretaciones resultan fácticamente verdaderas, verdaderas en el mundo, se obtienen modelos de la teoría formal. Los teoremas, dado que se deducen de los axiomas, también serán fácticamente verdaderos, y esas teorías serán ahora teorías fácticas. | Los axiomas de una ciencia formal son, en su conjunto, definiciones implícitas de los términos que contienen. Implícitas y parciales: se puede enriquecer esos términos con significados de los objetos del mundo y así obtener interpretaciones que se referirán al mundo. Si esas interpretaciones resultan fácticamente verdaderas, verdaderas en el mundo, se obtienen modelos de la teoría formal. Los teoremas, dado que se deducen de los axiomas, también serán fácticamente verdaderos, y esas teorías serán ahora teorías fácticas. | ||
La afirmación | La afirmación | ||
(x) x * n = x | (x) [x * n] = x | ||
(se lee: para todo x, x por n es igual a x) | (se lee: para todo x, x por n es igual a x) | ||
es verdadera en el contexto de la teoría de grupos. No es necesario que las afirmaciones de la matemática se refieran a algo que tenga alguna analogía con nuestra experiencia sensorial; los matemáticos se ocupan en teorías abstractas, y en muchos casos, como el de la teoría de grupos, les encuentran aplicaciones en las ciencias fácticas. | es verdadera en el contexto de la teoría de grupos. No es necesario que las afirmaciones de la matemática se refieran a algo que tenga alguna analogía con nuestra experiencia sensorial; los matemáticos se ocupan en teorías abstractas, y en muchos casos, como el de la teoría de grupos, les encuentran aplicaciones en las ciencias fácticas. | ||
La geometría del espacio real, la del espacio físico en el que vivimos, es una geometría física, una ciencia fáctica y sus afirmaciones deben ser compatibles | |||
La geometría del espacio real, la del espacio físico en el que vivimos, es una geometría física, una ciencia fáctica y sus afirmaciones deben ser compatibles | |||
Revisión actual - 22:25 10 nov 2015
El origen de las ciencias formales
¿Cuándo comenzó la ciencia? Una de las dificultades para responder a esta pregunta reside en cómo caracterizar esa forma de conocimiento que llamamos “ciencia”. Los filósofos de la ciencia han dado concepciones diversas de lo que ésta es. Podríamos reformular la pregunta así: ¿Cuándo y dónde apareció algo suficientemente parecido a lo que hoy llamamos “ciencia”? Los historiadores (al menos los occidentales: la ciencia, como hoy la conocemos, es una creación de Occidente) responderían “La ciencia comenzó en la antigua Grecia”. Aquellos griegos se reconocieron herederos de los conocimientos de las espléndidas civilizaciones de Babilonia y Egipto pero, además de incrementarlo enormemente, introdujeron la necesidad de sistematizarlo y justificarlo explícitamente. Los documentos históricos no dan indicios de que egipcios y babilonios hayan sentido una necesidad similar.
La ciencia según Aristóteles
Aristóteles de Estagira (Aristóteles) (siglo IV a. C.) fue un filósofo importante en su tiempo, pero es especialmente importante cuando consideramos la influencia que llegaría a tener más adelante. En la Baja Edad Media se impone la filosofía escolástica que integra en un mismo sistema las ideas de Aristóteles con las enseñanzas de la Biblia y la doctrina católica. Y se suponía que Aristóteles –“El Maestro”, como solía llamárselo– era casi tan infalible como la Biblia. El Renacimiento fue una época de explosión intelectual en la que se revalorizaron las obras de la antigüedad clásica en toda su diversidad. Pero el escolasticismo seguía siendo la filosofía de la Iglesia; los filósofos que crearon la ciencia moderna estudiaron en universidades en las que se enseñaba la ciencia aristotélica. La ciencia moderna no se pudo construir sobre la ciencia aristotélica sino en contra de ella. Sí, en cambio, hubo continuidad entre la concepción aristotélica de ciencia y la actual, especialmente en las ciencias formales: la lógica, una creación de Aristóteles (aunque él mismo no la consideró como una ciencia), y la matemática, una de las pocas disciplinas que no cultivó El Maestro. Aristóteles consideraba a la ciencia como un saber que la razón puede reconocer como cierto en sentido absoluto, opuesto al saber práctico del artesano (>>técnica y tecnología) y a la mera opinión sin fundamento. Las afirmaciones deben demostrarse mediante razonamientos a partir de otras afirmaciones ya conocidas como verdaderas. La lógica establece cómo justificar la validez de esos razonamientos. Aristóteles aceptaba que todo conocimiento es conocimiento acerca del mundo y que la generalización inductiva a partir de los hechos que observamos en el mundo nos acerca a los principios de la ciencia, pero no proporciona la certeza; esa es una tarea de la razón. Pero con un razonamiento se puede demostrar la verdad de una afirmación –la conclusión del razonamiento– cuando se parte de otras afirmaciones –las premisas– que se sabe que son verdaderas. No es posible demostrar todas las afirmaciones sin caer en un regreso al infinito o en circularidad. Algunos enunciados, los más simples, los más básicos, los primeros principios de una ciencia, son indemostrables, pero nuestra razón los acepta como verdaderos porque son intuitivamente evidentes. Los axiomas son comunes a todas las ciencias, tienen un alcance universal y se auto justifican por su evidencia; su verdad se impone a nuestra intuición como necesaria; por ejemplo: El todo es mayor que la parte [de ese todo] Quien no sea capaz de comprender esto, ¿cómo podría comprender algo acerca de cualquier ciencia? (Más adelante volveremos sobre esta afirmación). Los postulados son específicos de cada disciplina; son en cierto sentido “menos evidentes”, pero debemos aceptarlos como verdaderos porque sin ellos el resto de la disciplina no podría ser construida. Sin embargo, los autores posteriores también los aceptaron como verdaderos por su evidencia. (Actualmente se aplica la palabra “axioma” también para los postulados). Así como no se pueden demostrar todas las afirmaciones, y por motivos análogos, tampoco se pueden definir todos los términos. Los términos primitivos designan las entidades más básicas a las que se refiere una ciencia y su significado se comprende sin necesidad de explicación. En los principios se encuentran contenidas todas las afirmaciones de una ciencia pues, una vez aceptados, la coherencia exige que aceptemos todas las afirmaciones que se deducen de ellos: los teoremas. El primer ejemplo de aplicación de estas ideas lo encontramos en la geometría que construyó Euclides, que vivió en Alejandría hacia el año 300 a. C.
La geometría euclidiana
El tratado de Euclides conocido como los Elementos es uno de las obras más exitosas de la historia; hasta el siglo XIX fue usado como libro de texto y su modo de exponer la ciencia, lo que hoy llamamos “sistema axiomático”, fue imitado en las disciplinas más diversas (con mayor o menor éxito). Los primeros seis de sus trece libros tratan sobre geometría plana y comienzan con 23 definiciones de los términos que emplea, cinco postulados y los axiomas (entre cinco y once, según los distintos comentaristas). Luego da las demostraciones de 465 teoremas. Algunos de esos teoremas nos resultan tan obvios que no parece que fuera necesario demostrarlos, por ejemplo, Si dos rectas se cortan, forman ángulos opuestos por el vértice iguales entre si Pero en un sistema axiomático todas las afirmaciones son expuestas explícitamente como axiomas o postulados o bien deben estar rigurosamente demostradas a partir de ellos. Esta es la geometría que estudiamos en la escuela (aunque los alumnos actuales no soportarían la forma como la expuso Euclides); es la que corresponde a nuestra concepción intuitiva del espacio, que nos vamos formando desde que somos bebés, y es la que usamos cuando tenemos que, por ejemplo, calcular la cantidad de azulejos que necesitamos para revestir el cuarto de baño de casa. Es también la que se emplea en la ciencia y la tecnología para… casi todas sus necesidades. Esta geometría fue considerada como, simplemente, la geometría que describe el espacio en el que vivimos. Los filósofos racionalistas la consideraron el ejemplo más claro de que podemos adquirir conocimiento del mundo empleando solamente nuestra razón: no hace falta hacer experimentos para demostrar las afirmaciones de la geometría.
El quinto postulado
Se esperaba que los postulados expresaran verdades tan evidentes que estuviera claro que no es necesario demostrarlos; por ejemplo, el primer postulado dice:
Desde un punto a otro se puede trazar una línea recta
Pero ese no parece ser el caso del quinto postulado:
Si una línea recta al caer sobre otras dos forma ángulos en el interior y del mismo lado de la secante menores [su suma] que dos rectos [180 º], las dos rectas, indefinidamente, se encuentran en aquella parte en la cual los ángulos son menores que dos rectos.
Así lo formuló Euclides. No es sólo la dificultad de traducir fielmente algo escrito hace más de dos milenios; simplemente, no tiene la “obviedad” de los otros cuatro postulados; es difícil entenderlo sin la ayuda de un dibujo.
Muchos matemáticos pensaron, entonces, que no se trataba de un auténtico postulado sino de un teorema que podría ser demostrado a partir de los otros cuatro. A lo largo de los siglos fueron varios los matemáticos que buscaron esa demostración. El primero fue, quizá, Posidonio de Apamea en el siglo I a. C. Y lo consiguió, pero a costa de introducir otro postulado:
Las rectas paralelas son equidistantes
Esta historia se repitió varias veces más, siempre con el mismo resultado: se lo puede quitar de la lista de postulados pero reemplazándolo por otro. La versión más empleada actualmente es conocida como “postulado de las paralelas”:
Por un punto exterior a una recta pasa una y sólo una paralela a dicha recta
¿Es esta afirmación necesariamente verdadera?
Las geometrías no euclidianas
No son infrecuentes en la historia de la ciencia los casos de descubrimientos independientes y casi simultáneos. En el siglo XIX Carl Friedrich Gauss, János Bolyai y Nikolai Lobachevsky también intentaron demostrar el quinto postulado de Euclides empleando la misma estrategia: la demostración por reducción al absurdo. Se trata de tomar como premisas los cuatro primeros postulados y la negación del quinto, que en este caso fue Por un punto exterior a una recta pasa más de una paralela a dicha recta Luego se intenta deducir de ellos un enunciado de la forma “p y no p” (“p ∧ ~p”, siendo p cualquier enunciado); esta es una contradicción, que es necesariamente falsa; si se logra hacerlo, queda demostrado que el quinto postulado puede deducirse a partir de los otros cuatro. Consiguieron demostrar teoremas muy extraños pero no encontraron ninguna contradicción. Sin embargo no creyeron haber fracasado sino todo lo contrario: creyeron que los primeros cuatro postulados de Euclides y la negación del quinto constituyen una geometría distinta, una geometría que describe un mundo en el cuál, a diferencia de la geometría euclidiana, por un punto exterior a una recta pasan infinitas paralelas a dicha recta, la suma de los ángulos interiores de un triángulo vale menos de 180 º y la relación entre la circunferencia y su diámetro es mayor que π; un mundo que no es éste y que no cabe en nuestra imaginación, pero que no es un mundo lógicamente imposible. Hoy se la conoce como geometría de Lobachevsky (fue el primero en publicarla, en 1829).
En 1854 Bernhard Riemann desarrolló otra geometría no euclidiana en la que por un punto exterior a una recta no pasa ninguna paralela a dicha recta, la suma de los ángulos interiores de un triángulo vale más de 180 º y la relación entre la circunferencia y su diámetro es menor que π; en esta geometría el espacio es finito pero sin límites, sin bordes, y también sin centro. No es el espacio finito de la cosmología aristotélico-ptolemaica que sí tiene un límite –la esfera de las estrellas fijas– y un centro –el lugar donde está la Tierra–. Muchos matemáticos de la época consideraron a las geometrías no euclidianas como meros juegos que no eran dignos de aparecer en publicaciones científicas; las tildaron de “caricatura geométrica”, de “manifestación morbosa de la geometría”. Gauss, el primero que tuvo la idea, fue precavido y no publicó nada “por temor al griterío de los beocios [tontos]”. Evidentemente la geometría verdadera tenía que ser la de Euclides; las otras no podían ser más que meros “ejercicios lógicos”.
El espacio físico
En nuestro andar por el mundo consideramos el espacio y el tiempo como algo “dado”, como el marco en el que ocurren los hechos que podemos observar y que nos brindan información acerca de cómo es este mundo. El espacio y el tiempo son como la escenografía de una obra de teatro: el marco en el que se desarrolla la acción, que es lo que nos interesa. Hasta el siglo XIX, ése era también el papel del espacio y el tiempo en la investigación científica; no parecía que pudiera irse más allá de la especulación filosófica en estos temas. Pero sí era posible: en 1915 Albert Einstein publica su teoría general de la relatividad. Según esta teoría, espacio, tiempo y materia son interdependientes, no existe uno sin los otros. Si es correcta teoría del "big bang" (que presupone la relatividad einsteiniana) el espacio real, el espacio físico en el cual existimos, es finito pero sin centro ni límites. La mejor aproximación a la geometría del universo considerado como un todo es la geometría de Riemann, no la de Euclides. ¿Cómo puede algo ser finito pero no tener algo en el medio ni terminar en algún lugar? Nuestra intuición nos dice que eso no puede ser, pero, ¿es infalible nuestra intuición?, ¿no nos dice nuestro sentido común que la Tierra es plana y que no se mueve? Aceptamos sin protestar que la Tierra es redonda y se mueve alrededor del Sol porque nos lo repitieron varias veces en la época de nuestra vida en la que no se nos ocurriría dudar de lo que nos decía nuestra maestra de la escuela primaria. Los filósofos y los científicos no pueden permitirse esa actitud acrítica; pueden, en cambio, hacer el esfuerzo de reeducar sus intuiciones de sentido común. Pero nuestra intuición tiene un límite. Las teorías de la física moderna, las que aparecieron a principios del siglo XX, la relatividad y la cuántica, nos dicen que la realidad supera las posibilidades de nuestra imaginación. Éste fue uno de los motivos por el que fueron muy resistidas en su momento. Ahora, los científicos aceptan que las teorías científicas que se refieren al mundo pueden ir más allá de nuestra intuición. Es necesario, por supuesto, que sea posible inferir de ellas consecuencias observacionales (El método hipotético- deductivo) que permitan someterlas a contrastación; eso es lo que las permite calificarlas como ciencias fácticas. Es interesante el caso del “evidente” axioma 5 de Euclides: “El todo es mayor que la parte”. En 1874, Georg Cantor mostró que esa afirmación no puede justificarse cuando se trata de conjuntos infinitos, tema de casi toda la matemática. Por chocante que suene, debe admitirse que hay tantos números naturales (el todo) como números naturales pares (la parte). ¿Por qué habría de extrañarnos que nuestra intuición falle cuando nos las vemos con lo infinito? (También Cantor fue incomprendido por sus contemporáneos; algunos lo trataron de loco, y hasta de blasfemo por intentar introducir en la ciencia el infinito, uno de los misterios de Dios). Pero, entonces, ¿la geometría de Euclides es falsa?
Ciencias formales y ciencias fácticas Si decimos que esto
5
es un cinco, deberíamos decir que esto
hipopótamo
es un hipopótamo. Pero no, no decimos que es un hipopótamo, decimos que es un signo que usamos para hablar de los hipopótamos, unos animales grandotes que se bañan en los ríos de África y llegan a vivir hasta 30 años. Con el mismo criterio, entonces, deberíamos decir que “5” es un signo que usamos para referirnos... ¿a los cincos? ¿Y cómo son los cincos? ¿Son grandes o pequeños?, ¿dónde se bañan los cincos?, ¿cuánto tiempo vive un cinco? El desarrollo de la lógica y la matemática en la segunda mitad del siglo XIX y principios del XX ha conducido a una distinción tajante entre ciencias formales y ciencias fácticas. Las ciencias formales –la lógica y la matemática– no tienen contenido fáctico, no se refieren a hechos que podamos observar, no dicen nada acerca de la realidad, acerca del mundo. Los cincos no existen en la realidad, al menos no en la realidad en la que encontramos los objetos que existen en el espacio y en el tiempo, que podemos ver y tocar, como los hipopótamos, los ríos de África y el dedo meñique de nuestra mano izquierda. Necesitamos de la experiencia de la realidad para acceder al conocimiento de la matemática: empezamos aprendiendo a contar con los dedos de nuestra mano. No puede ser casualidad que la mayoría de los sistemas de numeración en las distintas lenguas tengan base diez, como también los hay de base cinco y de base veinte. Los antiguos egipcios desarrollaron una matemática práctica diseñada para las necesidades de su agrimensura y su arquitectura. Los antiguos griegos consiguieron despegarse de la realidad sensible y elaboraron una matemática abstracta desligada de toda aplicación; se interesaron, por ejemplo, en que cinco es un número primo o que se puede demostrar que sólo existe un poliedro regular con caras de cinco lados (el dodecaedro); ellos descubrieron la demostración, noción central de las ciencias formales. Las ciencias fácticas pretenden darnos información acerca de cómo es el mundo, y la aceptación de sus enunciados requiere de la experiencia, de los hechos (datos) del mundo que podemos observar. Pero nunca podemos asegurar que esos enunciados sean verdaderos; siempre serán hipótesis (hipótesis), aunque confiemos en ellas la eficacia de un tratamiento médico o la seguridad de un viaje en avión. De acuerdo con la concepción actual de las ciencias formales, podemos estar absolutamente seguros de que, por ejemplo, cinco más cinco son diez, si aceptamos que eso no dice nada acerca del mundo, que los cincos no están en el mundo. Pero, entonces, ¿qué son los cincos?, o mejor, ¿qué es el cinco? Y, ¿en qué sentido es verdad que cinco más cinco son diez? Los tratados sobre este tema generalmente adoptan una posición formalista: las ciencias formales contienen fórmulas “vacías”: los signos que las forman no se se refieren a nada, no significan nada. La palabra “verdad” está impuesta por la costumbre pero significa sólo “se deduce de los axiomas”. Actualmente no se admite la evidencia intuitiva como criterio de verdad, al menos en una ciencia. Sin embargo, algunos filósofos de la matemática sostienen la realidad de un “mundo” no espacial ni temporal en el que existen las entidades de la matemática como el cinco y el pentágono. Esa realidad no es accesible a los sentidos pero sí a la razón. Aquí, ya que no pretendemos ser muy rigurosos, adoptaremos una posición cómoda para nuestra intuición: los signos de una ciencia formal son creaciones abstractas de nuestra mente y sus enunciados son verdaderos en virtud cómo definimos esos signos, es decir, son verdaderos por convención. Es por convención que aceptamos como verdaderos enunciados como “Los unicornios tienen un cuerno en la frente”, y “Los centauros tienen cola de caballo” aunque nadie haya visto un unicornio ni un centauro. La afirmación de la geometría euclidiana Desde un punto a otro se puede trazar una línea recta es verdadera simplemente por lo que significan “punto” y “línea recta” en el contexto de la geometría euclidiana. La afirmación de la geometría riemanniana Desde un punto a otro se puede trazar más de una línea recta es verdadera por lo que significan “punto” y “línea recta” en el contexto de la geometría riemanniana. Y en el contexto de cualquiera de esas geometrías, la afirmación Desde una línea recta a otra se puede trazar un punto es falsa, si es que tiene algún sentido. Los axiomas de una ciencia formal son, en su conjunto, definiciones implícitas de los términos que contienen. Implícitas y parciales: se puede enriquecer esos términos con significados de los objetos del mundo y así obtener interpretaciones que se referirán al mundo. Si esas interpretaciones resultan fácticamente verdaderas, verdaderas en el mundo, se obtienen modelos de la teoría formal. Los teoremas, dado que se deducen de los axiomas, también serán fácticamente verdaderos, y esas teorías serán ahora teorías fácticas.
La afirmación (x) [x * n] = x
(se lee: para todo x, x por n es igual a x) es verdadera en el contexto de la teoría de grupos. No es necesario que las afirmaciones de la matemática se refieran a algo que tenga alguna analogía con nuestra experiencia sensorial; los matemáticos se ocupan en teorías abstractas, y en muchos casos, como el de la teoría de grupos, les encuentran aplicaciones en las ciencias fácticas.
La geometría del espacio real, la del espacio físico en el que vivimos, es una geometría física, una ciencia fáctica y sus afirmaciones deben ser compatibles